VoxEU Column COVID-19 Health Economics

Reproduction numbers tend to 1 and the reason could be behavioural

Joshua Gans
/

31 Aug 2020

Standard epidemiological models that show how infection rates in the population rise and then fall assume that people do not understand what’s going on. When people react to infection rates by changing behaviour, the model’s predictions are no longer valid. This column explains why that can mean that pandemics don’t rage out of control but become something more endemic. In particular, epidemiological models that incorporate rational economic agents tend to predict that pandemics may move towards a steady state for a significant period of time.

Joshua Gans

Professor of Strategic Management and Jeffrey S. Skoll Chair of Technical Innovation and Entrepreneurship, Rotman School of Management University Of Toronto

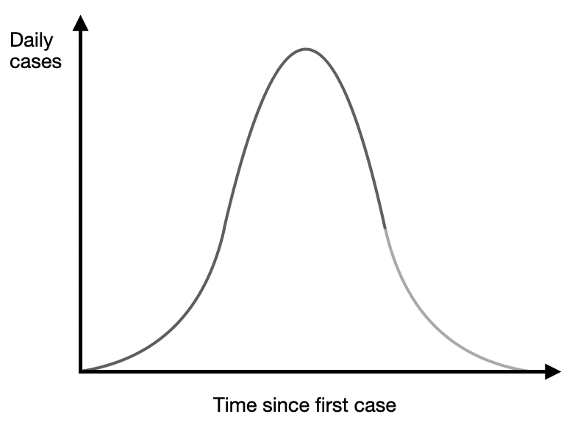
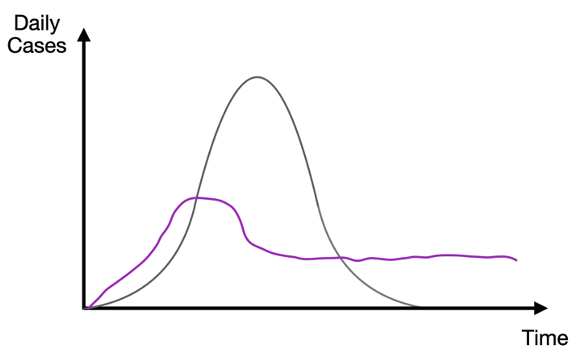
The graph below shows the baseline prediction of an epidemiological model where infected people who recover from a virus are immune thereafter. Notice that the share of the population who are infected at any given time rises from zero to a peak and then falls thereafter. The peak point, where the growth rate in the number of new daily cases turns from positive to negative, is the point at which herd immunity has been achieved. Beyond that point, there are too few people who are still susceptible to the virus to become infected in numbers greater than those who are recovering, and so the total number of infected people starts to drop off. That is the herd immunity threshold (Atkeson 2020).

What is really important is that such a point can be identified for those models if you know R0 — the basic reproduction number — which is the number of people someone who becomes infected with Covid-19 will themselves infect. The peak point arises when a share of people who are not immune is equal to 1/R0; that is, 1 - 1/R0 have been infected. For Covid-19, R0 was estimated between 2.5 and 3.5. (For something like measles, it is more like 12-18 and for influenza 1.5-1.8). Thus, the peak point of infections for Covid-19 would involve one third of the population (assuming R0 = 3) before dropping off to claim another third before it died out. If you can intervene and drive R0 down (by, say, social distancing or mask-wearing) and keep it there, you decrease the herd immunity threshold and so the number of people who at some point are infected.

R0 is the reproduction number that contains the ‘potential’ for the outbreak and how bad it might get. Overtime, the effective reproduction rate — how many people are added to the pool of infected compared to how many are removed (through recovery or death) — changes. It is denoted Rt or simply R. When R > 1, there are more people being added to the infected pool than removed and so prevalence — how many people are dangerous — is rising. When R < 1, the reverse is true. The figure above has R > 1 until a peak is reached and then R < 1 after that. Thus, the peak is at a point where R = 0 or there is no change in the size of the infected pool. Standard epidemiological models allow for public interventions (lockdowns, mask-wearing, testing) to push R down but the path of the virus if left alone follows the single speak, up and then down, prediction. (See Berger et al. (2020) for a clear formal exposition and Gans (2020a) for a longer discussion.)

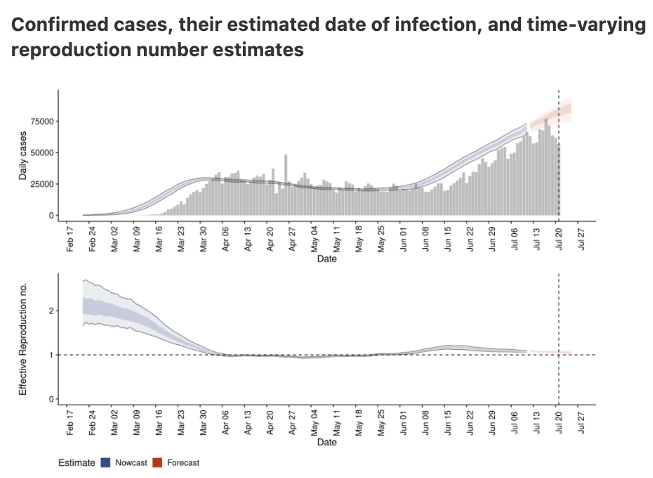
Where are we at the moment? For the US, to date, there have been 4.5 million recorded cases for Covid-19, or 1.3% of the population. So it does not seem like the US is anywhere near herd immunity based on epidemiological estimates of R0. This isn’t surprising because while R0 may be high, policies and other changes had an impact too. Thus, if we look at how the US has fared we get a graph like this (from epiforecasts.io):

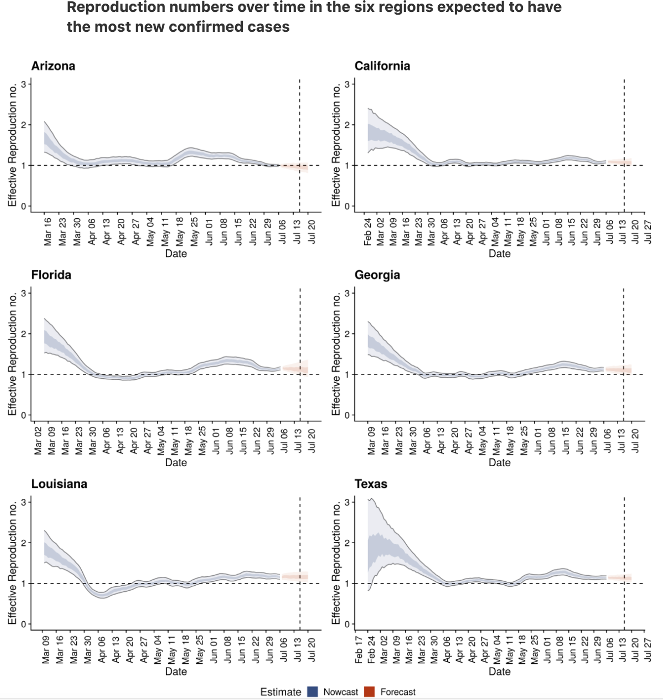
Notice that Covid-19 started out at an R of about 3 but quickly fell to 1 and has stayed around that level even during the additional and more significant outbreaks that happened in June and July throughout Florida, Texas, Arizona and California.

Thus, if you had followed a standard epidemiological model, your prediction for Covid-19 would have been incorrect. But, of course it would. We all reacted in March and behaviour changed. Some of this was by virtue of policy, such as the very strong lockdowns in New York or the take up of mask-wearing later on. But US policy interventions have been far weaker post-May. There is more going on here. Indeed, this pattern of R falling to about 1 happens across all states in the US and many countries in the world. To be sure, some countries actually suppressed the outbreak with R falling to 0 but for the majority, movement around 1 or just below it seems to be the norm. This regularity has been carefully documented by Atkeson et al. (2020).

What really happened?

What happened was people are people and when they know they can catch an infectious disease by physical contact they adjust their behaviour accordingly. Perhaps the clearest study of this comes from Goolsbee and Syverson (2020). They use mobile phone data to track visits to 2.5 million businesses in the US between March and May 2020. And they pay particular attention to counties that were in lockdown states that are next to counties in non-lockdown cases.

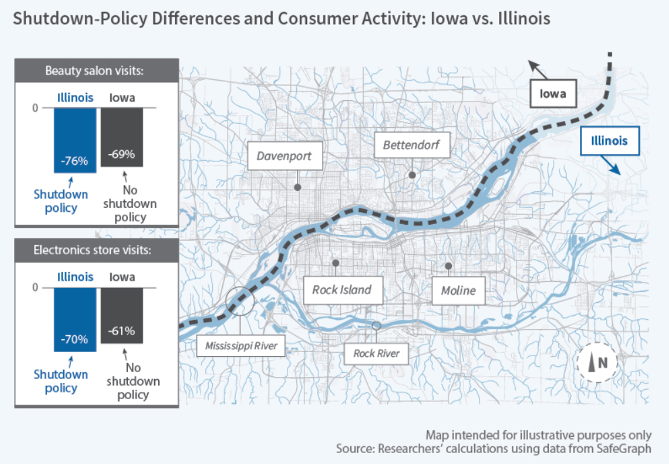
Here is an illustration of that for Illinois (lockdown) versus Iowa (no lockdown).

You can see here that having a government-mandated lockdown did mean fewer visits to various store types in Illinois but the difference was small compared to the reductions in visits that were as a result of peoples’ choices. Basically, overall activity seemed to drop by 60% on average but legal restrictions probably only accounted for 7% of that. Moreover, this traffic drop-off started before those restrictions were even in place. As it turns out, people were changing their behaviour more than just rushing for scraps of toilet paper. People also seemed to be reacting more to deaths near to them than just infections per se. Likewise, when counties started to ‘open up’, the increases in visits were modest.

There are several recent papers that use behavioural assumptions – namely, rational economic agents of the type pioneered by Gersovitz and Hammer (2004) – that show what this means for the path of the virus (Toxvaerd 2020, McAdams 2020, Gans 2020b). People generally condition their behaviour on how likely certain activity is likely to get them infected. So, when prevalence is high and there are relatively more infected people ‘out there,’ people will cut back on physical interactions and take more care to protect themselves. What does that do? It pushes R down and with it the size of the pool of infected people. By contrast, when prevalence is low, people relax and take more risks. That pushes R up again and so infections start to rise again. In the end, there is a tendency towards an equilibrium point where R = 1 and the size of the infected pool is stable. In that situation, people settle into their behaviour and the end result is that the growth in the virus is mitigated. The bad news, of course, is that the opposite occurs when the virus is on the decline, reversing that work. Thus, human behaviour leads to a situation where the virus just persists — that is, is endemic for some time. Thus, what really happened is more like the purple line drawn below.

What will see is something like this but then also, because small effects can sometimes lead to large changes, occasional outbreaks that bump R back up for a time before a change in behaviour wrestles the outbreak back towards a steady state. So expect a bumpy ride until there is a vaccine or some stronger, coordinated government action.

When people understand that there is a dangerous coronavirus circulating, they engage in behaviour that reduces the rate at which they are infected even without governments ordering them to do so. That’s the good news.

And now… the bad news

The bad news is that these people who react to what the virus is actually doing and similarly going to react when governments put in place various policies. If the government puts in policies that cause people to ‘stay in place’ and have law enforcement patrolling the streets as they did recently in Melbourne, then there isn’t much scope for people to react. But what if we engage in more modest policies such as testing, tracing and isolating which reduces the risk of being infected if you go out or we encourage mask-wearing with a similar desired effect? In that case, because their risk equation changes, people’s behaviour might change and this may have the perverse effect of increasing infection rates or, more assuredly, not reducing them by as much as might be hoped.